401: Linear Regression
Regression and Linear Classifiers
Traditional linear regression (a.k.a. Ordinary Least Squares) is the simplest and classic form of regression.
Given a linear model in the form of:
\begin{align} f(\mathbf{x}) & = w_0 + w_1x_1 + w_2x_2 + \dots \\ & = \mathbf{w} ^T \cdot \mathbf{x} \end{align}
Linear regression finds the parameters \(\mathbf{w}\) that minimises the mean squared error (MSE)…
The MSE is the sum of the squared values between the predicted value and the actual value.
\begin{align} MSE(\mathbf{w}) = \frac{1}{m} \sum_{i=1}^{m}{(\mathbf{w}^T \cdot \mathbf{x}^{(i)} - \mathbf{y}^{(i)})^2} \end{align}
Where \(m\) is the number of observations.
Cost function
- The MSE is known as a cost function.
We can also use a measure of how good a fit is (utility or fitness function).
- We can then tweak the parameters to minimise the cost function
???
The typical use for a cost function is to measure how badly a model fits or classifies the data. The model is then tweaked to minimise the cost function. E.g. For linear regression we often use the distance between the predictions from the model and the real data; the MSE in the previous example.
Normal equation
There is a closed solution to find the optimal MSE for a given data. It’s called the Normal equation.
\begin{align} \hat{w}=\left(\mathbf{x}^T\cdot\mathbf{x}\right)^{-1} \cdot \mathbf{x}^T \cdot \mathbf{y} \end{align}
Let’s generate some synthetic data and run through this manually.
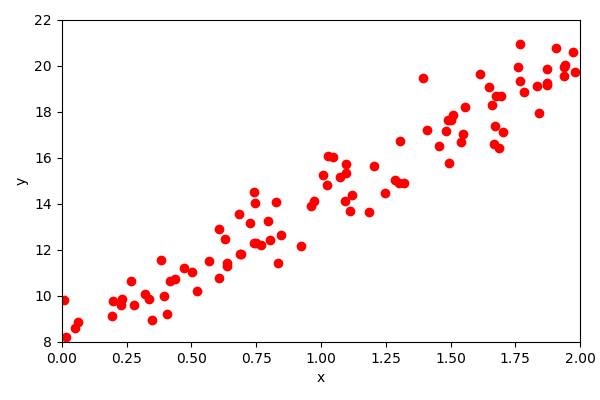
Linear regression
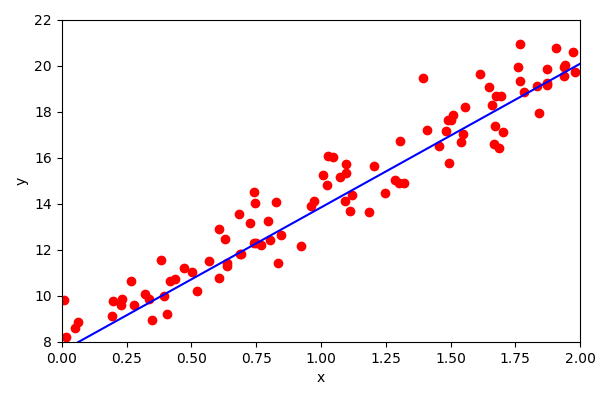
Most of the time you will use a library, but sometimes you need to dig deeper.
???
Most standard models and optimisers are already implemented. During your day-to-day work you will use these. But it aids understanding and occasionally you will need custom implementations.
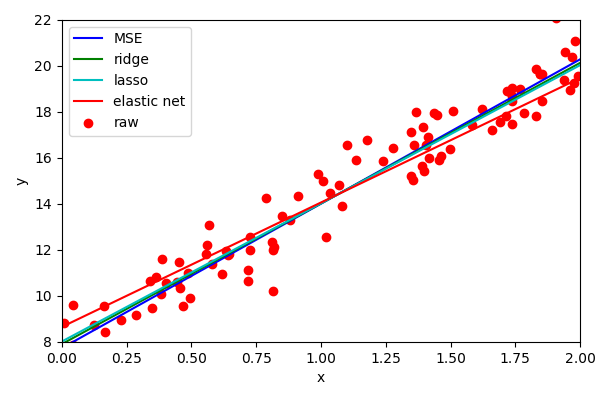
Other Regression
- Ridge regression (penalises the squared weights - regularisation)
- Lasso regression (penalises absolute magnitudes of the weights)
- Elastic Net regression (combination of Ridge and Lasso)
???
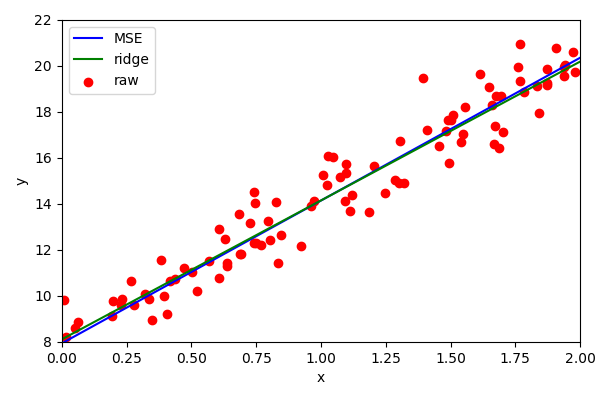
Ridge regression
Other linear regression implementations exist. Ridge regression attempts to optimise the same parameters but penalises the squared weights.
Effectively it attempts to minimise the use of features. This is called regularisation.
Ridge regression is most useful when there are large numbers of features.
Lasso regression
Another type of regression is called Lasso. This is similar to Ridge regression but penalises L1 (absolute) magnitudes of the weights.
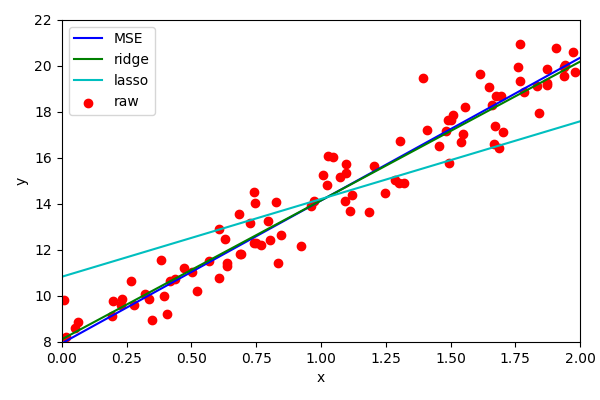
We can see that the penalty is too aggressive. We can alter the alpha parameter to reduce the
the aggressiveness of the penalisation (same for Ridge).
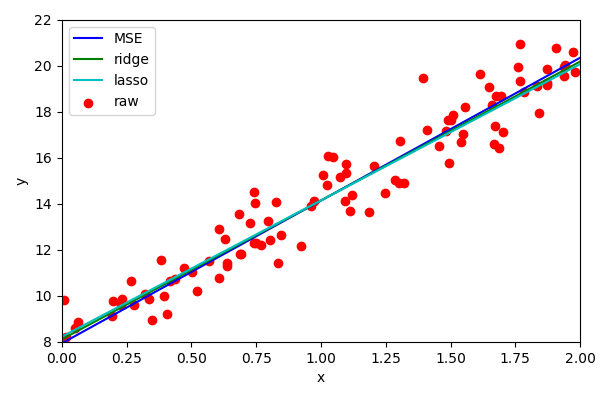
Generally, Ridge regression is simpler to use but assumes Gaussian noise. Lasso performs better when there are outliers (due to the L1 penalisation, rather than L2).
Elastic Net
There is one final common form of regularisation and that is called Elastic Net. In essence, it is a combination of both ridge and lasso regression, where you can control the level of influence from each.
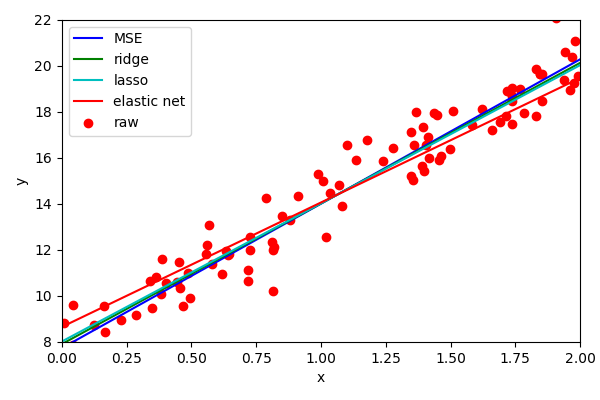
We can see that the effect is quite pronounced.
RANSAC
RANSAC randomly picks a selection of observations from the sample and then performs regression as normal.
The most common set of parameters are chosen as the final result.
This algorithm works really well when there are outliers in the data.
When would you use what?
- Avoid plain linear regression
- Ridge is a good default
- Avoid ridge if the data is grossly non-normal
- But if only a few features are useful, prefer lasso or elastic
- Avoid lasso and use elastic with large numbers of features, or correlating features
- RANSAC whenever you have outliers that you don’t want to get rid of.